Wind Speed & Direction (Ultrasonic Anemometer 2D).
Speed of Sound
The speed of a sound wave in air depends upon the properties of the air,
namely the temperature and the pressure. At normal atmospheric pressure, the
temperature dependence of the speed of a sound wave through air is approximated
by the following equation:
v = 331.45 m/s + (0.6 * T)
where T is the temperature of the air in degrees Celsius.
Since the speed of a wave is defined as the distance which a point on a wave
(such as a compression or a rarefaction) travels per unit of time, it is often
expressed in units of metres/second (abbreviated m/s). In equation form, this
is:
speed = distance / time
The Ultrasonic Anemometer 2D is designed to detect the horizontal
components of wind velocity and wind direction as well as the virtual
temperature in two dimensions.
The Ultrasonic Anemometer 2D consists of 4 bi-directional ultrasonic
transducers, in pairs of 2 which are opposite each other at a distance of 250
mm.
The transducers act both as acoustic transmitters and acoustic receivers.
The respective measurement paths and their measurement direction are
selected via electronic control. When a measurement starts, a sequence of 4
individual measurements in all 4 directions of the measurement paths is
carried out at maximum speed.
The measurement directions (acoustic propagation directions) rotate
clockwise, south to north, west to east, north to south and east to west.
Wind velocity and direction
When the sound wave travels against the wind, the total transit time is
increased by a wind speed dependent amount. When the sound wave travels with
the wind, the total transit time is reduced.
The different wind speeds and directions are measured over a fixed path.
As the speed of sound is very dependent on the air temperature, the
propagation time of the sound is measured on both of the measurement paths in
both directions. In this way, the influence of the temperature
dependent speed of sound on the measurement result can be eliminated by
subtracting the reciprocals of the measured propagation times.
By combining the two measuring paths which are at right angles to each
other, one obtains the measurement results of the angle and velocity of the
wind.
The time of flight of the first signal (out) is given by:
to = d / (c + v) (1)
where:
d is the distance between the transducers (0.25m).
c is the speed of sound.
v is the wind speed along the transducer axis.
t is the time taken.
The time of flight of the third signal (back - opposite direction) is given by:
tb = d / (c - v) (2)
The windspeed, v, along any axis can be found by inverting the above
relationships, then subtracting (2) from (1):
These formula's assures that the wind speed does not depend on pressure,
temperature and humidity.
Orthogonal ultrasonic anemometer 2D design

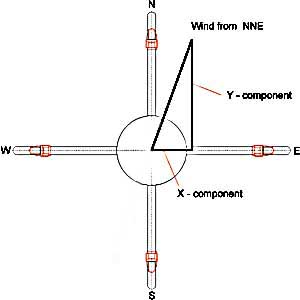
x = (d / 2) * (1 / twe - 1 / tew)
y = (d / 2) * (1 / tsn - 1 / tns)
If wind direction is exactly in line with one measuring path (NS or SN or WE or EW), this will cause
turbulence due to transducer structure. This will cause erratic readings and needs to be compensated for
in software
Equilateral triangle ultrasonic anemometer 2D design

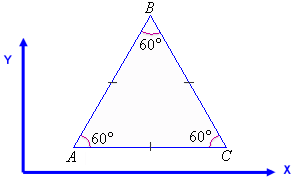
ab = (d / 2) * (1 / tab - 1 / tba)
bc = (d / 2) * (1 / tbc - 1 / tcb)
ca = (d / 2) * (1 / tca - 1 / tac)
Add only the two most reliable vectors that are not affected by turbulence around transducers,
by using trigonometry to obtain the x and y components
Add vectors AB and CA
x = ab * Cos (60) + ca
y = ab * Sin (60)
Add vectors AB and BC
x = ab * Cos (60) + bc * Cos (60)
y = ab * Sin (60) + bc * Sin (60)
Add vectors BC and CA
x = bc * Cos (60) + ca
y = bc * Sin (60)
If all three vectors are not affected by turbulence around transducers, add vectors AB, BC and CA
x = ab * Cos (60) + bc * Cos (60) + ca
y = ab * Sin (60) + bc * Sin (60)
Magnitude and direction calculated from x and y coordinates
The length of the vector r pointing from the coordinate origin to a point
in 2D space is given by Pythagoras' Theorem
r = sqrt(x2 + y2)
While the polar or phase angle f is obtained by performing the
operation:
First quadrant (+x, +y)
f = 90 - arcsin (y / r)
Fourth quadrant (+x, -y)
f = arcsin (y / r) + 90
Third quadrant (-x, -y)
f = (90 - arcsin (y / r)) + 180
Second quadrant (-x, +y)
f = arcsin (y / r) + 270
Wind speed at above angle:
v = r m/s
or:
v = r * 3.6 km/hr
or:
v = r * 1.9476 knots
Virtual Temperature
As previously mentioned, the speed of the propagation of sound is highly
dependent on the air temperature, but is hardly affected by air pressure and
humidity.
As this is a measurement of gas temperature which is made without thermal
coupling to a measurement sensor, it is called the "virtual temperature".
The advantages of this measured variable is the avoidance of measurement
errors such as those which occur when a solid state temperature sensor is
heated up by sun irradiation or cooled by evaporation cooling by rain and
wind.
The sonically determined speed of sound can be found from the sum of
the inverses of (1) and (2):
c = (d / 2) * (1 / to + 1 / tb)
The sonic virtual temperature, in degrees Celsius is given by:
Ts = ((c * c) / (1.4 * 287.04)) - 273.15
| Temp ( o C) |
Speed of Sound (m/s) |
0 km/hr |
1 km/hr |
50 km/hr |
100 km/hr |
| Time out (us) |
Count (decimal) |
Time back (us) |
Count (decimal) |
Time out (us) |
Count (decimal) |
Time back (us) |
Count (decimal) |
Time out (us) |
Count (decimal) |
Time back (us) |
Count (decimal) |
Time out (us) |
Count (decimal) |
Time back (us) |
Count (decimal) |
| -10 |
325.19 |
768.78 |
3075 |
768.78 |
3075 |
768.13 |
3072 |
769.44 |
3077 |
737.29 |
2949 |
803.08 |
3212 |
708.28 |
2833 |
840.59 |
3362 |
| 0 |
331.31 |
754.58 |
3018 |
754.58 |
3018 |
753.95 |
3015 |
755.21 |
3020 |
724.22 |
2896 |
787.60 |
3150 |
696.21 |
2784 |
823.63 |
3294 |
| 10 |
337.32 |
741.13 |
2964 |
741.13 |
2964 |
740.52 |
2962 |
741.74 |
2966 |
711.83 |
2847 |
772.96 |
3091 |
684.75 |
2738 |
807.64 |
3230 |
| 20 |
343.23 |
728.38 |
2913 |
728.38 |
2913 |
727.79 |
2911 |
728.97 |
2915 |
700.06 |
2800 |
759.10 |
3036 |
673.85 |
2695 |
792.52 |
3170 |
| 30 |
349.03 |
716.27 |
2865 |
716.27 |
2865 |
715.70 |
2862 |
716.84 |
2867 |
688.86 |
2755 |
745.95 |
2983 |
663.47 |
2653 |
778.20 |
3112 |
| 40 |
354.74 |
704.74 |
2818 |
704.74 |
2818 |
704.19 |
2816 |
705.29 |
2821 |
678.19 |
2712 |
733.46 |
2933 |
653.56 |
2614 |
764.61 |
3058 |
Distance is 0.25m at clock rate 16.0MHz / 4 = 4.0MHz (0.25us)
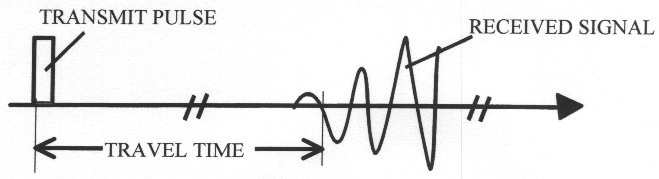
Measurement process (from transmit pulse to first zero crossing)
A number of zero crossing samples will need to be taken to see if they are valid or noise.
After each zero crossing, the amplitude increases for a number of cycles, before decaying away
on the received signal. Using a fast ADC (analog to digital converter - e.g. dsPIC30F series), this
received digitized signal is processed for a number of samples after each zero crossing, looking for
this characteristic increase in amplitude and not the decrease in amplitude from a ringing (oscillating)
transducer after the transmit pulse (crosstalk) or structure borne ultrasound.
The final received signal is a mixture of body signal (decaying), ringing from previous received or transmitted signal (decaying) and
received air signal (increasing then decaying).
This will cause the proceivied start of the received air signal to appear stretched, shrunk or in phase, so the zero crossing point will
continually change at this point causing jitter and not a fixed measurement.
The received signal (measure a number of timing of zero crossings and amplitudes) is passed through a mismatched filter (compares received
signal to template of reference signal increasing in amplitude) and extract the wanted air signal to win back the actual starting point.
A mismatch filter is achieved using the weighting filter with the application of adaptive weighting coefficients for side lobe suppression
in cascade behide a matched filter.
Dug this up (If the template (reference signal) for the convolution isn't exactly a replica then the filter might be said to be "not
matched" or "mismatched"). True or false ?
Orthogonal ultrasonic anemometer / Equilateral triangle ultrasonic anemometer
TAD = ((1/16000000) * (4 + 1)) / 2 = 156.25 ns
Sampling freq = 1 / ((0.00000015625 * (12 + 1)) = 492308 Hz / 246154 Hz
One cycle of 40kHz = 1 / 40000 = 25 us
Number of samples = 0.000025 / (1 / 492308) = 12 / 6
Project is on hold at present - what looks good on paper does not all ways work in practice. Due to a lot of factors altering the final
outcome. Will get back to it in near future with fresh ideas, new circuit and brushed up on complex mathematics for digital signal
processing (DSP).
Any ideas, e-mail to trekker@netspace.net.au
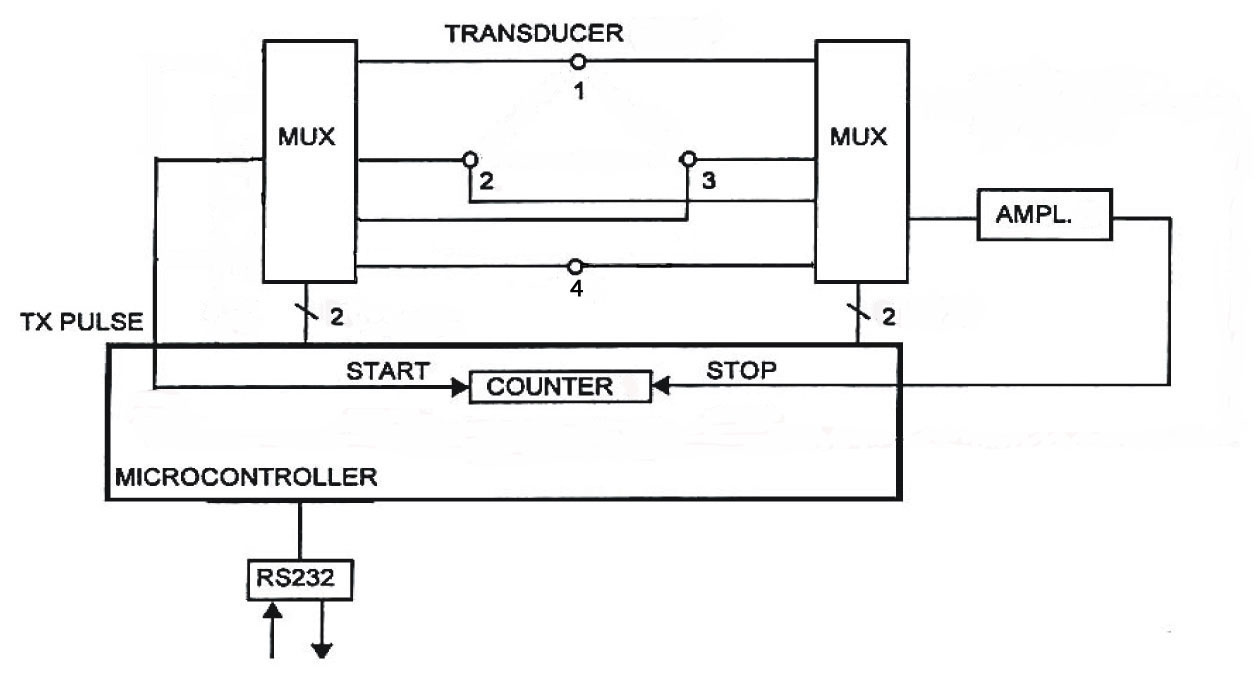
Orthogonal ultrasonic anemometer block diagram
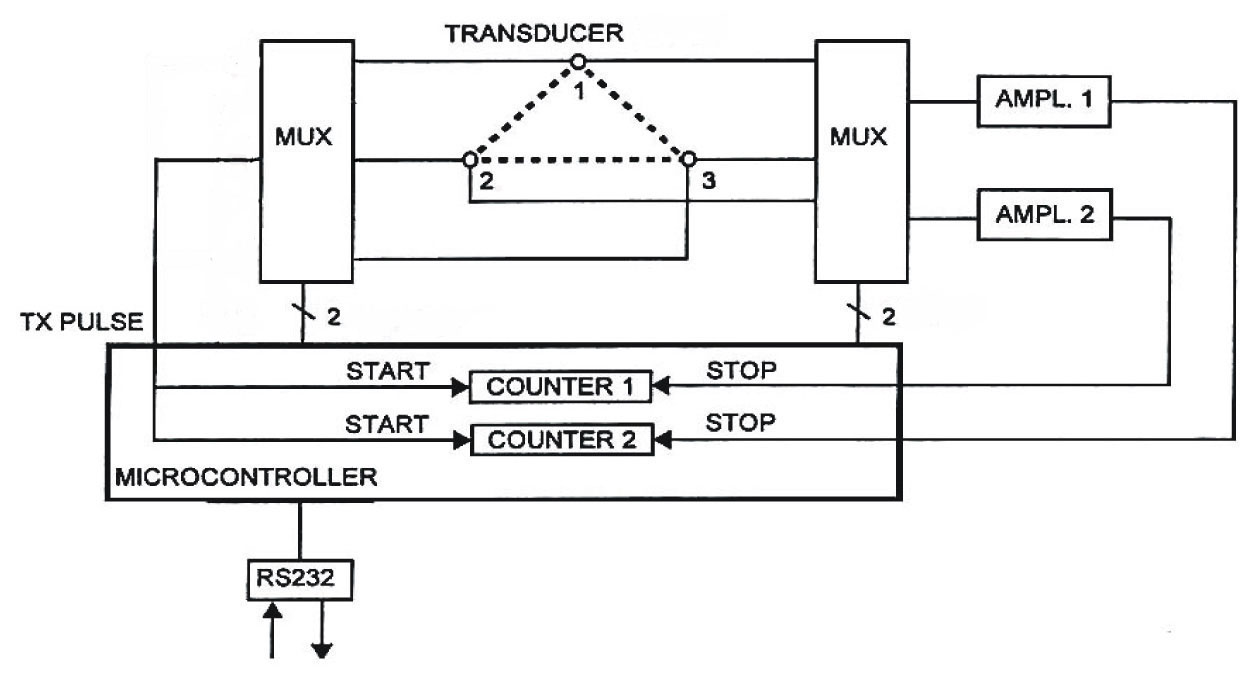
Equilateral triangle ultrasonic anemometer block diagram
Suppliers of ultrasonic sensors.
The following ultrasonic sensors work.
MA40E8-2 (14mm Dia), Willow Technologies (US$16.95 each + US$20.00 shipping).
MA40E8-2 (14mm Dia), Murata.
The following ultrasonic sensors have not been tested for suitability (use at your own risk).
MA40E6-7 (18mm Dia), Willow Technologies.
MA40MC10-1B (10mm Dia) or MA40E6-7 (18mm Dia), Murata.
T/R40-12H (12mm Dia), T/R40-14A (14mm Dia), T/R40-18D (18mm Dia), Audiowell Electronics (Guangzhou) Co.,Ltd.
BPU-1640IFAH10.5S (16mm Dia), BPU-1840IFAH12 (18mm Dia), BPU-1840IFAH14S (18mm Dia), Bestar Electronics Industry Co Ltd.
40CA-18SC (18mm Dia), APC International Ltd.
40CA-15E (15mm Dia) or 40CA-18E (18mm Dia) or 40CA-18SC (18mm Dia), Ceramic Transducer Design Co.,Ltd.
HE240STR (27mm Dia - 3/4" NPT - US$79.00 each), Hexamite.
HX40STRC (18mm Dia) or HX40STRE (26mm Dia - 3/4" BPT), Hexamite.
40KPT18A (18mm Dia), Senscomp.
18A/40 (18mm Dia), Massa.
UTEC4014 (14mm Dia) or UTEC4016 (16mm Dia) or UTEC4018 (18mm Dia), Sencera Co. Ltd.
400EP125 (12.5mm Dia) or 400EP18A (18mm Dia), Prowave.
The following ultrasonic sensors do not work.
Excessive ring time that swamps out the received signal.
The distance between the ultrasonic transducers will need to be increased from 250mm to ???mm to compensate.
Low output level (increasing distance will only make matters worse).
AU-5550, T/R40-16B (16mm Dia), Jaycar (AU$4.95 each).
T/R40-16B (16mm Dia), Audiowell Electronics (Guangzhou) Co.,Ltd.
Notes.
Use the combined use type (bi-directional) not the receiver and transmitter type.
The use of open structure types will eventually fail due to the effects of the
weather.
The ultrasonic transducers need to have a short ringing time < 0.5ms at 5v.
The ultrasonic transducers need to have a minimum detectable range of 0.2 m or less.
How to Draw an Equilateral Triangle
1. Draw a line segment with your ruler.
2. Put the point of your compass at one end of the segment and the pencil point at the other.
3. Without moving the point of the compass and without changing how wide it is set, swing the
compass in approximately a quarter-circle (up & away from the line segment).
4. Without changing how wide the compass is spread, move the compass point to the other end of segment.
5. Swing the compass so that the arc you are creating crosses the arc you drew in step 3.
6. Mark the place where the two arcs cross. This is the apex of your triangle.
7. Using a ruler, draw line segments that connect the spot where the arcs cross to each end of the
original line segment.
Multiple feedback bandpass filter
fc = 40kHz
gain = 4
bandwidth = 12kHz
C = 220pF
Q = 40000 / 12000 = 3.32
R1 = 3.32 / (4 * 2 * 3.142 * 40000 * 220 x 10-12) = 15k ohms
C' = (220 x 10-12 * 220 x 10-12) / (220 x 10-12 + 220 x 10-12) = 110pF
R3 = 3.32 / (2 * 3.142 * 40000 * 110 x 10 -12) = 120k ohms
R' = 1 / ((2 * 3.142 * 40000)2 * 120000 * 220 x 10-12 * 220 x 10 -12) = 2725.8 ohms
R2 = (15000 * 2725.8) / (15000 - 2725.8) = 3.3k ohms
What others have built.

Wind Speed Meter,
as published in Everyday
Practical Electronics (EPE) Magazine, January 2003 -
Program -
Schematic 1 and
2 -
Original article
Wind Sonic, Sylvain - Canada)
Sonic Anemometer
Ultrasonic Anemometer, Hardy - Germany
Ultrasonic Anemometer, Hardy - Germany (Fantastic website now in english)
Ultrasonic Anemometry Anyone -
Circuit Cellar May 2001 issue 130 by Gordon Dick
- Program
Internet-Connected Sonic Anemometer (three point) -
Circuit Cellar Jan 2006 issue 186 by Ingo Cyliax
WeBBS Remote Weather Station
Anemometer Digital Ultrasonic - Brasil
Design of a 1-D Sonic Anemometer
Orthogonal sonic anemometer 2D design
Reference.
How does an Anemometer Work?
Active bandpass filter calculator
Speed of sound in some common material's
Understanding crosstalk in analog multiplexers
Analog Switches and Multiplexers Basics
Sonic Anemometry for the Hobbyist - Byte Magazine July 1979 Vol.4 Iss.7 Pg.120 by Neil Dvorak -
schematics and programs (for copies of this article, contact your
local library
or magazine publisher)
A microprocessor based, three axes, ultrasonic anemometer by A Alberigi Quaranta 1985 - Italy
ASTM D5527 - 00(2007) Standard practices for measuring surface wind and temperature by acoustic means
ASTM D6011 - 96(2003) Standard Test Method for Determining the Performance of a Sonic Anemometer/Thermometer
Vector Component Addition Example
Digital Signal Processing (DSP) tutorial
A complete book on DSP
PIC Microcontoller DSP Math Methods
Numerical Recipes in C, The Art of Scientific Computing, Chapter 12 Fast Fourier Transform, Chapter 13 Fourier and Spectral Applications
FFT Guru
Illustrates a recursive fast Fourier transform (FFT) algorithm
Basic and Optimized Goertzel's Algorithm
Matched Filter
Matched Filter
dsPIC DSC DTMF generation library and detection library using Goertzel's algorithm
dsPIC30F2010-20E/SP (ZZ8575)
Olimex PIC-PG1
or PIC-PG2 serial programmer
- WinPic software
- dsPIC 30F series processors adapter
dsPIC/PIC programmer (KC-5467) - Siliconchip - May 2008
- Modified schematic
- WinPic software
PICkit 2 Programmer/Debugger
- Junebug PK2SE Programmer/Debugger
Alternatives.
Wind Speed & Direction Meter using a hall effect sensor (UGN3503U)
pdf
Program
PCB
DIY Rotorvane Anemometer
Thermal anemometer
Return to weather station page.







